Evades Unraveled
Table of Contents [+]
Class: All Classes
Faction: All Factions
Level: All Levels
Item Links:
Quicklink (copy this):
Feedback: Please Login first
Table of Contents:Faction: All Factions
Level: All Levels
Item Links:
Quicklink (copy this):
Feedback: Please Login first
I. Introduction
II. Methodology
III. Results and discussion
IV. Additional considerations
V. Editor's Comment and Summary
VI. References
⇑
I. IntroductionAfter (irregularly) playing AO for nearly a decade and getting one character to 220/30 and multiple others to TL5/6, I was still mostly clueless about the mechanic of evades. Here are some unanswerable questions to illustrate this:
- If one has to choose between increasing evades and other useful skill, how exactly one can do that without knowing quantitatively what evades do?
- When one has 3000 evades, does additional +20 (say from IGoC that sells for 1+ billion!) make any measurable difference or not?
- Is there any difference between many different “flavors” of evades: individual (Dodge/Evade/Duck), combined one - AddAllDef, and another combined type – DefenseModifier?
- Why Jobe clusters have percentage sign in description (as in, % Add All Def.), yet DefenseModifier as listed effect?
This is rather confusing. There are number conflicting opinions about (in)equivalency of various evades, but hardly any solid information available in public forums. And that does not even touch upon a much bigger question:
How do Attack Rating (AR) and Defense Rating (DR) translate into probability (P) of landing a hit?
Let's start with definitions. The AR is simply a numerical value listed in attacker's stats window. The DR is not listed directly anywhere. For the purpose of this study, DR is defined as an arithmetic sum of appropriate defense skill and AAD[1] (AddAllDef) modifier. For example, if attacker uses pistol with "Defence skills: Dodge-Rng 100%" and defender has total Dodge-Rng skill 350 listed in skills dialog (which includes bufs, armor and implants), wears 1000 Tokens board, which has 60 AAD, and wears no additional AAD pieces, the DR is 350+60=410. Please see the section IV for the justification of summing skill and AAD.
The probability of landing [P] is defined as fraction of shots that land to total number of shots taken, provided that the number of shots is large. Mathematically speaking, it is a limit of such fraction for the number of shots going to infinity. In plain example, if you were to shoot mob 10 time and hit 3 times, the fraction would be 0.3. If you continue shooting, and do 100 shots, the fraction very likely deviates from initial 0.3. When you consider what happens with fraction as you increase number of shots, you expect the fraction to converge to some value, which is the probability.
The lack of any solid understanding of the relationship between AR, DR (+ some other unknowns) and P, is what prompted Threezey to write “In my opinion, the evade formula is the last, and only true mystery left in the game”[1]. I completely share his opinion. Threezey not only states this grand deficiency in 2008, but also preformed and disclosed some research that was aimed to solve the mystery. Unfortunately, his study did not yield the tangible conclusion. In his own words, “I excel graphed the hell out of them, calculated the error values, etc etc and didn't find any easy-to-identify patterns”.
So that was my starting point. Let’s see if the mystery still remains.
⇑
II. Methodology.For this study, I’ve used primarily two froob characters – Aigen (lvl 164 agent) as a hitter and Kuracup (lvl 170 fixer) as a punching bag. The choice is based on the availability and on the fact that Kuracup had token board and both GA1 and GA2, which made it possible to sweep DR range 66 to 2000+ quite easily with one skill reset. Juggling implants and various armor pieces made it possible to quickly vary DR and AR. To get even lower than 66 DR and 145 AR, I rolled two new trader characters.
To determine probability fairly accurately, one needs many shots. How many? Again, Threezey stated it correctly: “at least 1000 attack attempts, in order to get a more correct percentage, not due to random chance. Ideally 10,000”. On average, I did 4600 shots per experiment in ~90 separate tests. It took quite a few weeks real time. It may seem like overkill, but it turned out to be quite essential in order to get to useful final result. It also produced absolutely priceless expression on my wife’s face when I explained to her exactly why I am regularly leaving computer on overnight.
To simplify the system and save time I made an choice to restrict this study to AggDef slider set at full Def for my punching bag and to full Agg for my hitter.
⇑
III. Results and discussion.The obtained probabilities are lumped together in Figure 1. Despite the large average number of shots, the data does not look very pretty. I feel that there is some additional element that is pseudo-randomly chosen by the engine not on a per shot basis, but per “starting the attack” event or even per log in event. Something in a spirit of a proc, perhaps. However, it is just a feeling and I cannot substantiate it mathematically. Be that as it may, the range of the data set appears to be sufficiently large so that this additional variable(s) would not be able to obfuscate the actual DR/AR/P relationship.
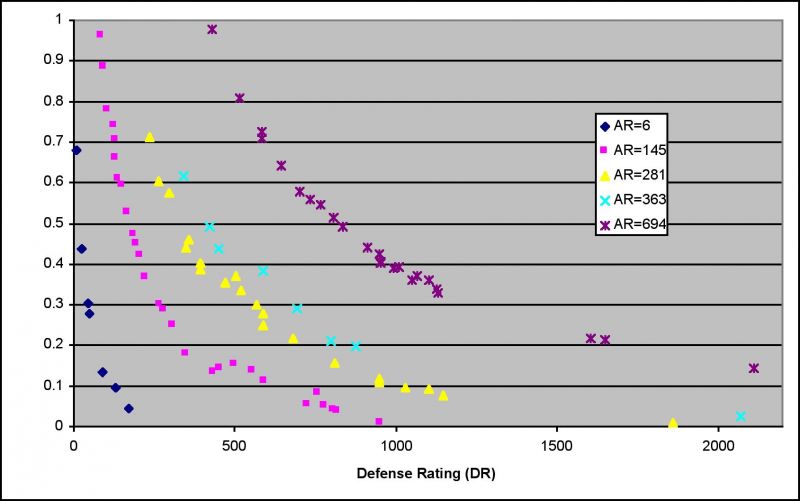
Figure 1. To-hit probabilities as functions of DefenceRatings for different AttackRatings.
There are two additional elements to this data, which are omitted in Figure 1. It turns out that for every AR there is a DR value, going above which produces no hits at all. That was demonstrated by doing 10000+ experiments in a few cases. That is a very non-obvious result. Many games employ mechanics that puts lower bound on probability to hit, say at 5%. So whatever you do, there is at least 5% chance to be hit. AO is different in that respect. Same thing about upper bound, which appears to be missing as well (100% probability to hit appears to be possible), but I did not spend much time on that subject.
The interesting thing about no-hits DRs and ARs is that they are reproducible to the point of being exact. For example, combination of 2514 DR and 363 AR results in no hits, yet 2513 DR and 363 AR has at least 0.005 probability of landing a hit. If one plots DR vs AR for the limiting cases(i.e., where DR is large enough but no larger to reach complete invincibility = zero probability to land a hit), one observes a rather striking picture: a perfect (notice that r2=0.99996) linear correlation as depicted in Figure 2.
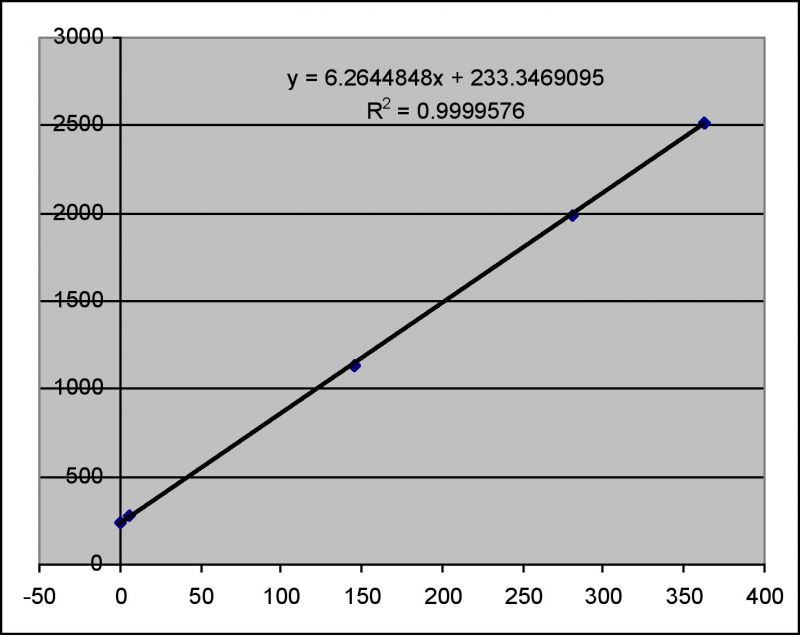
Figure 2. Minimum DR vs AR for p=0 condition.
I will not go into gory detail of how shape of curves in Fig. 1 and Fig. 2 eventually led me to come up with an equation that does well to encompass all the data. Suffice it to say that I eventually arrived to equation of the following form
| p = a * (AR + k) / (DR + l) + b | (1) |
where a, b, k, l are independent parameters. Fitting all four parameters results in a pretty good agreement between data and predictions. However, the relationship shown in Figure 2 is not reproduced well. To reconcile the data with “exactness” of relationship shown in Figure 2, one can reduce the number of parameters in equation (1) to only two (I chose b and k), while the other two are calculated from fit parameters in Figure 2 combined with b and k. Doing that guarantees that the fitted parameters in equation (1) would produce not only a reasonable approximation to data shown in Figure 1 but also exactly conform to Figure 2.
So, without further ado, here is the final equation:
| p = 0.6944 * (AR + 45.85) / (DR + 38.89) - 0.11317 | (2) |
And the full data set from Figure 1 is re-plotted in Figure 3 as experimental value vs predicted value:
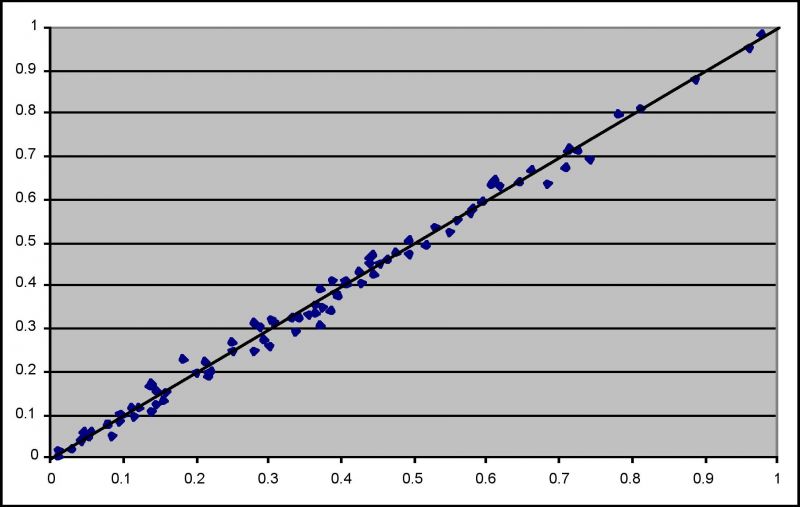
Figure 3. Experiment vs prediction with equation (2).
The standard deviation in prediction is only 0.013 (as in, if “true” p = 0.5, there prediction will be in range 0.500 +/- 0.013 in 68% of cases, assuming a normal/Gaussian distribution). In plain language, the equation (2) is pretty good predictor, at least in the range we considered.
As additional validation, I applied this equation that Threezey’s results:
| AR =1900; DR=3269 (2209+1060); p=0.2798 and AR =1900; DR=3269 (1729+1540); p=0.3076 |
Equation (2) predicts 0.2955, which is an excellent agreement, even without considering that Threezey’s data is way outside the range of ARs I used to determine the equation (2).
⇑
IV. Additional considerations.It would seem that the goal of finding the relationship between AR/DR and landing-a-hit probability has been successfully achieved (for now at least or until developers change the mechanics). I’ll leave AggDef slider effects for the future and for whoever decides to unravel that. I personally play with full-Def pretty much all the time.
I’ve also examined my data set to see whether AddAllDef and regular evades are equivalent. I can say that the Pomidor’s hypothesis [2] that AAD works as percentage added to base evades has no merit. For example, AR=694; DR=1104 (Duck=234; AAD=870) results in 0.36 fraction of landed hits. For the same AR=694; DR = 1127 (Duck=876; AAD=251) results in 0.34 fraction, which means the results are statistically indistinguishable – consistent with nearly identical DR. If we were to believe Pomidors hypothesis, the respective DRs would be very different 438 (=234+0.87*234) and 1096 (876 + 876*0.251) and so would be the probabilities. This is clearly not the case. Nonetheless, there is not enough information to conclude that AAD and regular evades are identical in all respects. It is possible that there are differences that lie elsewhere, critical hit change, landing perk chance, etc. Again, this is a subject for some other day and probably some other person.
If you like this study and find it useful, send a tell to say so in-game to one of the mentioned characters, Aigen or Kuracup. That will be some additional justification for the time I spend with this project.
Cheers and Happy playing!
⇑
V. Editor's Comment and SummaryHi, this is Llie. For people who didn't follow the careful experiment that Aigen performed to completely solve the AR/DR equation, I wanted to summarize his findings and highlight the important facts. (Think of this as a TL;DR for this guide)
First of all, in order to compute your DR for use in Aigen's formula, you need to know your current evade and your total ADD. You can obtain the appropriate evade/dodge/duck skill from the IP window. If you do not know your total AAD or would rather not have to figure it out by adding all the AAD equipment your character has equipped. You may view your AAD by creating the following script in your Scripts folder:
<a href="text://<a href=skillid://277>Addall-Def</a>">Click to Open Window</a>
Run the script in a chat window and click on the links to obtain your current AAD.
Secondly, thanks to Aigen's research we now have a definitive formula for how often, on average an attacker will land a hit given the attacker's attack rating and the target's defense rating (which is computed by Equation 2 above). You can use this formula for estimating your twink's ability to land hits on typical opponents, your tank's likeliness to be hit by typical opposing forces, and the total damage over time your weapons will do. Using this formula will provide you with a much better estimate than any previous attempts to estimate these things. (For the non-math people, the result is a number between zero and one. You multiply it by 100 to get a percentage. So for example, if you plug in numbers and get p=0.5, when you multiply by 100, you get that you will hit your target -- on average -- 50% of the time.)
Finally, the formula and the findings show that there is a DR above which an attack with too-low an AR will never hit. This is very important as this may save you a lot of wasted effort attending raids or mass PvP where you have no hope of contributing to the damage.
⇑
VI. References1. http://forums.anarchy-online.com/showthread.php?t=528996
2. http://forums.anarchy-online.com/showthread.php?t=502184
Last updated on 12.14.2013 by Llie
Written by: Aigen (AKA Kuracup)
Edited and additional comments by: Llie
Do you have questions about this article or found an error? No comments yet - Please login first to post a comment.
Written by: Aigen (AKA Kuracup)
Edited and additional comments by: Llie
Do you have questions about this article or found an error? No comments yet - Please login first to post a comment.
